CQF机器学习:高维统计中过参数化为何能避免过度拟合?
来源:
网络
2022-05-10
一般学机器学习的都知道有个定理,就是说整体误差Mean Square Error(MSE)包括了Bias(偏差)和Variance(方差)两个部分,如果参数越来越多,那么Bias会越小,而Variance会越大。道理也很简单,因为参数越多,越容易拟合真实的向量,但每个参数的估计都带来一点随机性,整体方差当然就大了。
一般的最小二乘是无偏估计,为了降低方差,提高泛化能力,一般会牺牲精度,比如各种正则化方法都可以降低方差,但都会引入Bias。
但所有以上这些,都是在低维统计众的结论,也就是默认参数的个数p小于样本的数量n。
但到了高维统计,也就是p>n甚至p>>n的时候,也就是p远大于n的时候,以上结论有时候并不成立。
就好像牛顿力学,只在低速宏观物体运动中成立,但在高速微观运动中并不成立。机器学习、统计学其实跟统计物理有类似的地方。
比如现在的机器学习中有个词叫做double descent,也就是所谓“双重下降”,指的测试误差随着参数个数的增加,一开始先下降,然后上升,这是传统机器学习的情况;但到了高维机器学习,某些情况下,随着参数的增加,它还会继续下降。
比如这是一幅比较经典的double descent的图:
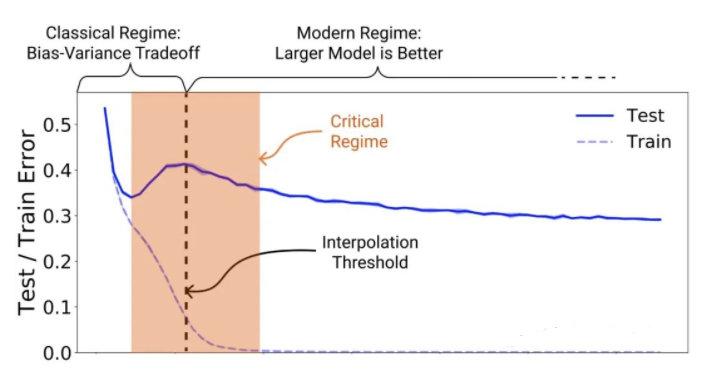
还有一些简化实验的图
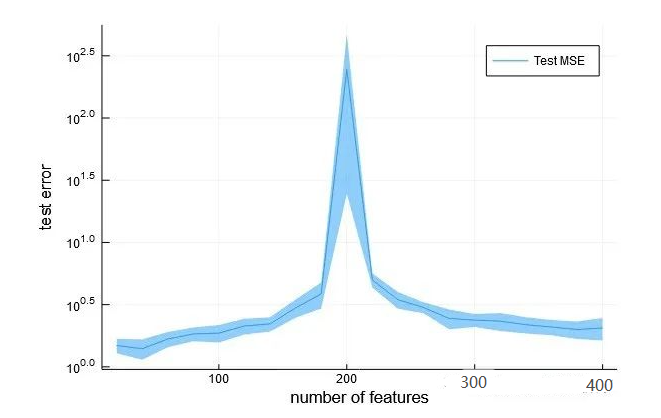
都可以看到,随着features(特征)的数目逐渐增加,测试误差先下降,然后增加,最后继续下降。
这个就具有很强大的现实意义,意味着人们不用担心训练集过度优化,不用担心大力出奇迹,不用担心过度拟合,只要成本可以支持,比如超级计算机够强大,内存足够大,完全可以拟合超级复杂的模型,参数越多越好,反正最后测试集误差也是会下降的。
主要的原因在于,比如p>>n,这里n=200,如果p=400,也就是特征数目是400,远大于样本数量。进一步假设,其中只有200个特征是有意义的,其它都是噪音;那么噪声变量越多,有意义的那部分特征只是一个更小的子空间,预测将越来越不准确,bias会越大,因为预测会越来越不准确;但同时,由于噪声多了,如果加入一定的正则化条件,那么分配给每个特征的系数绝对值会更小,也就是variance会更小,反而不容易过度拟合。
比如我找一篇雄文来说明一下,美国统计学总统奖得主、斯坦福统计系的大佬、统计学习圣经Elements of Statistical Learning的作者Tibshirani,他儿子小Tibshirani在一篇论文是这么写的:
看来美国也是阶层固化啊,统计学大佬的儿子继续搞统计,说不定未来也拿总统奖。学术垄断,世风日下。
回到正题,反正也说明我说的没错,还真有这事。因此,继续可以得到一些反直觉的结论:
- 数据不要太多。比如有200个特征,如果用1000个数据,那么是p>n,普通的低维统计;但如果用100个数据,就是p>n,变成高维统计了,高维统计就不怕过度拟合了。
- 可以尽情使用更多的参数和更复杂的模型。因为貌似大佬说最后测试误差还是会下降的,那么只要参数越来越多,大力出奇迹就可以的。
- double descent不是深度学习特有。
上面例子可以看出,普通的线性回归也会有这样的特性,所以也不要太迷信深度学习。结构太复杂,反而掩盖了事情的本质。
最后简单用R语言做一个实验来验证一下:
random_features <- function(n=100, d=100, num_informative_features=20) {y <- rnorm(n)X <- matrix(rnorm(n*min(d, num_informative_features)), nrow=n) + yif (d>num_informative_features)X <- cbind(X, matrix(rnorm(n*(d-num_informative_features)), nrow=n))return (list(X=X,y=y))library(lmeVarComp)set.seed(200)n <- 200ds <- seq(from=20, to=2*n, by=20)[-10]num_informative_features <- 1000nreps <- 10mses <- matrix(0, nrow=length(ds), nreps)train_errors <- matrix(0, nrow=length(ds), nreps)for (rep in 1:nreps) {mse <- c()train_error <- c()for (d in ds) {aa <- random_features(n,d,num_informative_features)Xtrain <- aa$Xytrain <- aa$yw <- mnls(Xtrain, ytrain)bb <- random_features(round(n/10),d,num_informative_features)Xtest <- bb$Xytest <- bb$ymse <- c(mse, sum((ytest-Xtest%*%w)^2))train_error <- sum((ytrain-Xtrain%*%w)^2)}mses[,rep] <- msetrain_errors[,rep] <- train_error}mean_mse <- apply(mses, 1, mean)plot(ds,mean_mse, type="l")
最后上图:
很明显看到了double descent,测试误差先下降后上升,在p=n会爆炸,这里图删除了那个点,否则会压缩的太厉害;然后p>n之后又继续下降了。
另外还可以看到训练集的误差是零,高维统计一般可以在训练集做到完美拟合:
mean_te <- apply(train_errors, 1, mean)plot(mean_te, type="l")
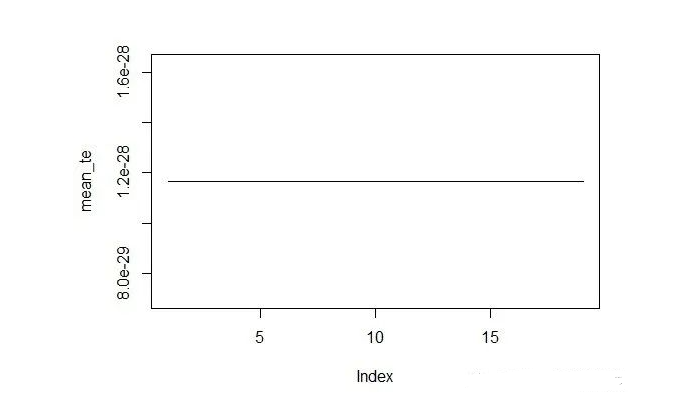
值得注意的是,这里求解使用了minimum norm least squres(mnls),这个不同于lasso,ridge和least squares,需要用到专门的包求解。由于p>n,普通的最小二乘无法求解,如果是lasso、ridge,似乎没有类似的效果。不清楚python有没有类似的包,Julia会更方便,直接就行。
对于量化交易的启示也类似,如果不怕过度拟合,那么建模是很容易的事情。当然,交易有风险,入行需谨慎,我也只是抛砖引玉。
版权声明:本条内容自发布之日起,有效期为一个月。凡本网站注明“来源高顿教育”或“来源高顿网校”或“来源高顿”的所有作品,均为本网站合法拥有版权的作品,未经本网站授权,任何媒体、网站、个人不得转载、链接、转帖或以其他方式使用。
经本网站合法授权的,应在授权范围内使用,且使用时必须注明“来源高顿教育”或“来源高顿网校”或“来源高顿”,并不得对作品中出现的“高顿”字样进行删减、替换等。违反上述声明者,本网站将依法追究其法律责任。
本网站的部分资料转载自互联网,均尽力标明作者和出处。本网站转载的目的在于传递更多信息,并不意味着赞同其观点或证实其描述,本网站不对其真实性负责。
如您认为本网站刊载作品涉及版权等问题,请与本网站联系(邮箱fawu@gaodun.com,电话:021-31587497),本网站核实确认后会尽快予以处理。
CQF备考 热门问题解答
- CQF考试难度大不大?
-
CQF考试的难度还是挺大的,因为CQF课程内容非常丰富,需要掌握的知识点非常多。CQF考试主要包括金融工程、计量金融、风险管理、计算金融等多个方面的知识,需要考生掌握才能通过考试。
- cqf一共几门几年考完?
-
cqf一共8门考试,考试的时间每个人都不同,如果考生基础较好的话,那么最快6个月通过所有考试,因为cqf考试的一个学习周期就是半年左右。如果考生的基础比较薄弱,那么通过考试的时间可能就会比较短了。
- cqf一年考几次?
-
cqf的考试一共有四次,每年完成相应的课程就可以考试了。学员可以在六个月内完成六个模块的学习并选修选修课,从而全面攻读该课程。此选项提供立即访问整个计划所需的所有材料以及终身学习。
- cqf的含金量如何?
-
cqf证书含金量是很高的,这一点毋庸置疑。cqf的课程内容不仅包含量化金融领域的基础知识,同时不断更新和吸收前沿的国际量化金融知识,其学习模块有好几种,分别是数据处理基础、量化投资多平台模拟交易、金融知识基础和Python语言编程基础等,内容这一块还是值得金融行业的人才学一下。
严选名师 全流程服务
其他人还搜了
热门推荐
-
CQF考试难不难?难度体现在哪儿? 2023-10-31
-
24年cqf报考条件要求是什么?附考试科目和内容 2023-10-30
-
2024年cqf考试报考条件公布了吗?考生速看! 2023-10-30
-
2024年CQF考试的费用标准是什么样的?学姐来给你解答! 2023-10-30
-
请注意!2024年CQF考试安排已确定! 2023-10-30
-
2024年CQF考试时间已定!考生须知! 2023-10-28
-
量化金融分析师考试时间已定!考生须知! 2023-10-27
-
量化金融分析师考试时间是什么时候?附详细表格! 2023-10-27
-
量化金融分析师考试难度大不大?一文全面解析! 2023-10-26
-
量化金融分析师考试费用一共得花费多少?费用汇总来了! 2023-10-26
-
CQF考试费用一共得花费多少?费用汇总来了! 2023-10-26
-
CQF量化投资分析师需要多少费用?速戳! 2023-10-20
-
CQF考试费用高吗?一共要多少钱? 2023-10-20
-
cqf新手必备科普文,看这篇就够了! 2023-10-17
-
cqf报名要求是什么?准备报考的看这篇! 2023-10-17
-
cqf报名要求是什么?准备报考的看这篇! 2023-10-17
-
cqf什么时候可以报名?不清楚的来看! 2023-10-16
-
24年cqf报名时间安排,看这篇就够了! 2023-10-16
-
24年cqf报考时间在几月?新手不要错过! 2023-10-16
-
2024年考cqf需要具备哪些条件?一篇文章讲述! 2023-10-16
-
2024cqf报名时间已出,一文掌握详情! 2023-10-16
-
cqf报考全面科普,新手不要错过! 2023-10-16
-
年薪100万真的很简单!考下1个证书就行了! 2023-10-14
-
CQF最新报名费用一览,国内外差距不是一点大! 2023-10-13
-
CQF报名一览:报名时间丨费用丨条件 2023-10-13
-
24年CQF必看!关于考试报名时间、入口及流程 2023-10-13
-
CQF啥时候考试?这篇说明白了~ 2023-10-13
-
千万不要在国外考CQF?看看学费就知道了! 2023-10-11
-
2024cqf的报考条件是什么?官方最新要求一览,速戳! 2023-10-10
-
24年cqf报考条件有哪些?点击了解! 2023-10-07
 更多服务
更多服务







































