学习过线性代数的同学,在学习到矩阵运算这一节的时候,一定看到过这个矩阵乘法的运算规则:

1、如何解线性方程组
解线性方程组,是我们从初中就学过的知识:
【例】:解三元一次方程组


2、如何用矩阵初等行变换的方法解线性方程组
在计算中,我们发现:这样的符号,在计算中完全可以省略,只要计算的时候,把每个未知数的系数位置明确即可。所以,以后这样的方程组之间的运算,就用矩阵的初等行变换来代替了:

矩阵第一行4个元素,从左到右依次表示第一个方程3个未知数的系数和等号右边的2。其他行也同理。(虚线只是方便区分系数和等号右边的数字,没有实际意义)
而我们前面解方程的过程,也简化为了对矩阵做初等行变换的过程:

经过一系列的初等行变换之后,矩阵变成了这样:

方程组自然就解出来了。
到这一步,你可能觉得已经很完美了,但是数学家觉得,这种方法还是不够简洁。
3、用矩阵记录初等行变换的过程
仔细观察矩阵初等行变换的过程:我们发现,把某行加到某行,把某行乘某个数,这些带有规则数字的内容,其实也可以表示为一个矩阵!
比如:

我们把这三串数字,按照顺序:对第1行的变换过程记录,就写在第1行,第2行的变换过程记录,就写在第2行:
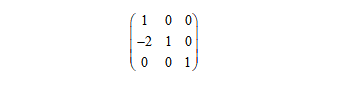
这个拼出来的矩阵,里面记录了上一次初等行变换的信息。
现在我们开始定义矩阵的乘法了:
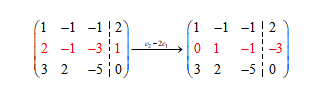
这个过程,现在就写成了(刚才那个记录变换过程的矩阵被放在了原矩阵的左边):
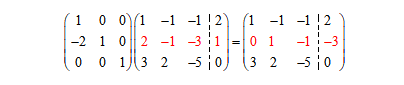
这样矩阵乘法的计算规则就很自然的被定义出来了。
为了表述方便,我们把这个乘法简记为:

4、解方程组,需要若干次初等行变换

这样一来,一个复杂的解方程组过程,用三个字母和一个等号简洁的表示出来了。
感兴趣的同学可以验算一下:

因为这里面是很多个初等行变换乘在一起的运算了,这个运算就不初等了。我们就只管他叫行变换好了。
当然,线性代数这门学科发展到今天,矩阵乘法的意义已经远远超出了解方程组这样简单的运用范畴了。如果单纯的考虑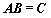 这样的矩阵乘法,我们发现,只要的
这样的矩阵乘法,我们发现,只要的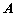 列数和
列数和 的行数相同,矩阵乘法就可以顺利的进行下去。
的行数相同,矩阵乘法就可以顺利的进行下去。
当然,线性代数这门学科发展到今天,矩阵乘法的意义已经远远超出了解方程组这样简单的运用范畴了。如果单纯的考虑
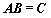 这样的矩阵乘法,我们发现,只要的
这样的矩阵乘法,我们发现,只要的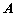 列数和
列数和 的行数相同,矩阵乘法就可以顺利的进行下去。
的行数相同,矩阵乘法就可以顺利的进行下去。
5、重点:不可以随意交换乘法的顺序

总结
聪明的你已经发现了:我们文章开头的那个看起来莫名其妙的求和项,只不过是把每一行的整体运算,拆解成了每个元素单独的运算:
展开全文
版权声明:本条内容自发布之日起,有效期为一个月。凡本网站注明“来源高顿教育”或“来源高顿网校”或“来源高顿”的所有作品,均为本网站合法拥有版权的作品,未经本网站授权,任何媒体、网站、个人不得转载、链接、转帖或以其他方式使用。 经本网站合法授权的,应在授权范围内使用,且使用时必须注明“来源高顿教育”或“来源高顿网校”或“来源高顿”,并不得对作品中出现的“高顿”字样进行删减、替换等。违反上述声明者,本网站将依法追究其法律责任。 本网站的部分资料转载自互联网,均尽力标明作者和出处。本网站转载的目的在于传递更多信息,并不意味着赞同其观点或证实其描述,本网站不对其真实性负责。 如您认为本网站刊载作品涉及版权等问题,请与本网站联系(邮箱fawu@gaodun.com,电话:021-31587497),本网站核实确认后会尽快予以处理。
考研热搜
-
2023暨南大学日语语言文学专业802翻译与写作考研试题! 高顿教育 2023-09-14 10:34:12

-
2023年暨南大学法语语言文学专业730综合法学考研试题! 高顿教育 2023-09-14 10:17:49

-
2023年暨南大学公共管理各专业717公共管理学考研试题! 高顿教育 2023-09-14 10:11:28

-
2023年暨南大学数学系709数学分析考研试题一览! 高顿教育 2023-09-14 10:01:25

-
2023暨南大学资产评估专业436资产评估专业基础考研试题! 高顿教育 2023-09-14 09:47:36

-
2024中国地质大学(武汉)计算机技术考研考哪些科目?附参考书目 高顿教育 2023-09-14 09:07:42

考研


证书星级










距离考研考试仅剩
天
全国硕士研究生统一招生考试,简称“考研”。是指教育主管部门和招生机构为选拔研究生而组织的相关考试的总称,由国家考试主管部门和招生单位组织的初试和复试组成。是一项选拔性考试。思想政治理论、外国语、大学数学等公共科目由全国统一命题,专业课主要由各招生单位自行命题(加入全国统考的学校全国统一命题)。硕士研究生招生方式分为全日制、非全日制、中外合办等。培养模式分为学术型硕士和专业型硕士研究生两种。
加载更多 













