I.考试大纲适用对象及考试性质
本大纲适用于重庆市普通高校“专升本”的理工类和经济类考生。
“专升本”考试结果将作为重庆市普通高校高职高专学生申请“专升本”的成绩依据。本科院校根据考生考试成绩，按照已确定的招生计划择优录取。因此，该考试应具有较高的信度、效度，必要的区分度和适当的难度。
II.考试内容与要求
一、一元函数微分学
1.理解函数的概念，知道函数的表示法；会求函数的定义域及函数值。
2.掌握函数的奇偶性、单调性、周期性、有界性。
3.理解复合函数与反函数的定义，会求单调函数的反函数。
4.掌握基本初等函数的性质与图像，了解初等函数的概念。
5.理解极限的概念及性质，掌握极限的运算法则。
6.理解无穷小量与无穷大量的概念及两者的关系，掌握无穷小量的性质和无穷小量的
比较。
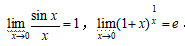
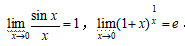
7.了解夹逼准则与单调有界准则，掌握两个重要极限：专升本试题
8.理解函数连续与间断的定义，理解函数间断点的分类，会利用连续性求极限，会判
别函数间断点的类型。
9.理解闭区间上连续函数的有界性定理、最值定理、介值定理，并会用上述定理推证一些简单命题。
10.理解导数的定义及几何意义，会根据定义求函数的导数。
11.理解函数的可导与连续的关系。
12.熟练掌握基本初等函数的导数公式、导数的四则运算法则、复合函数求导法则、隐
函数求导法、对数求导法及参数方程求导法，了解反函数的求导法则。
13.了解高阶导数的概念，熟练掌握初等函数的一阶和高阶导数的求法。
14.理解微分的定义、可微与可导的关系，了解微分的四则运算法则及一阶微分形式的不变性；会求函数的微分。
15.理解罗尔（Rolle）定理、拉格朗日中值（Lagrange）定理，了解柯西（Cauchy）中值定理和泰勒（Taylor）中值定理。会用罗尔定理证明方程根的存在性，会用拉格朗日中值定理证明一些简单不等式。
16.熟练掌握用洛必达法则求未定式的极限。
17.理解函数极值的概念、极值存在的必要条件及充分条件。
18.会求函数的单调区间和极值，会求函数的最大值与最小值，会解决一些简单的应用
问题，会证明一些简单的不等式。
19.了解函数的凹凸性及曲线的拐点的定义，会求函数的凹凸区间及曲线的拐点。
20.会求曲线的渐近线，会描绘一些简单函数的图形。
二、一元函数积分学
1.理解原函数和不定积分的概念及性质。
2.熟练掌握不定积分的基本公式。
3.熟练掌握不定积分的换元积分法和分部积分法。
4.理解变上限积分函数的定义，掌握求变上限积分函数导数的方法。
5.理解定积分的概念和几何意义，掌握定积分的基本性质。
6.熟练掌握牛顿-莱布尼兹（Newton-Leibniz）公式，掌握定积分的换元法和分部积分法。
7.掌握定积分的微元法，会求平面图形的面积及平面图形绕坐标轴旋转的旋转体的体积。
8.理解无穷区间上有界函数的广义积分与有限区间上无界函数的瑕积分的概念，掌握
其计算方法。
三、向量代数与空间解析几何
1.理解空间直角坐标系及向量的概念，掌握向量的坐标表示法，会求向量的模、方向余弦。
2.掌握向量的线性运算、向量的数量积、向量积的计算方法，理解其几何意义。
3.熟练掌握两向量平行、垂直的条件。
4.会求平面的点法式方程、一般式方程、截距式方程。会判定两个平面的位置关系。
5.了解直线的一般式方程，会求直线的对称式（点向式）方程、参数式方程。会判定
两条直线的位置关系。
6.会判定直线与平面的位置关系。
四、多元函数微积分学
1.理解二元函数的概念，会求一些简单二元函数的定义域。
2.了解二元函数的极限、连续的定义及其基本性质。
3.熟练掌握显函数的一阶、高阶偏导数的求法。
4.会求二元函数的极值，会用拉格朗日乘数法求条件极值。
5.熟练掌握二元函数全微分的求法。
6.熟练掌握二重积分的计算方法。
五、微分方程
1.理解微分方程的定义及阶、解、通解、特解等概念。
2.熟练掌握可分离变量的微分方程、齐次微分方程及一阶线性微分方程的解法。
3.理解二阶常系数齐次线性微分方程解的性质及通解的结构。
4.熟练掌握二阶常系数齐次线性微分方程的解法。
六、无穷级数
1.理解无穷级数收敛、发散的概念。
2.理解级数收敛的必要条件和级数的主要性质。
3.知道几何级数，级数的敛散性。
4.熟练掌握正项级数的比较判别法、比值判别法与根值判别法。
5.理解幂级数的收敛半径、收敛区间及收敛域的定义。
6.熟练掌握求幂级数的收敛半径、收敛区间及收敛域的方法。
七、线性代数
1.理解行列式的概念，掌握行列式的性质。
2.掌握行列式的计算。
3.会用克莱姆（Cramer）法则。
4.熟练掌握矩阵的线性运算及运算法则、矩阵的乘法及运算法则。
5.理解方阵可逆的概念和判定法则，掌握求可逆矩阵的逆矩阵的方法。
6.理解矩阵的秩的概念，掌握求矩阵秩的方法。
7.会解简单的矩阵方程。
8.熟练掌握矩阵的初等变换。
9.掌握齐次线性方程组有非零解的判定条件及解的结构，掌握非齐次线性方程组解的
判定和结构。
10.熟练掌握线性方程组的解法。
八、概率论初步
1.理解随机事件的概念，掌握事件之间的关系和运算。
2.了解概率的统计定义，掌握概率的基本性质和概率的加法公式。
3.掌握古典概率的计算公式，会求一些事件发生的概率。
4.理解事件独立性的概念，能用事件的独立性计算概率。
5.理解随机变量的概念，会求一些简单随机变量的分布。
6.理解随机变量的数学期望及方差的概念，掌握数学期望和方差的基本性质，会求一些简单随机变量的数学期望和方差。
*注：本大纲对理论、概念等从高到低的要求是：理解，知道，了解；对方法、计算等
从高到低的要求是：熟练掌握，掌握，会。
III.考试形式与试卷结构
一、试卷题型及分值分布
1.试卷题型
单项选择题、填空题、计算题、证明题。
2.分值分布
试卷总分为120分。
单项选择题约32分。
填空题约16分。
计算题约64分。
证明题约8分。
二、考试方式及考试时间
1.考试方式为闭卷笔试。
2.考试时间为120分钟。
【参考书目】
1.同济大学数学系高等数学（第六版）高等教育出版社
2.彭玉芳等线性代数（第二版）高等教育出版社
3.同济大学数学系概率论与数理统计（第2版）同济大学出版社


展开全文