Ⅰ.考试内容与要求
本科目考试要求考生掌握高等数学的基本概念、基本理论和基本方法，主要考查考生识记、理解、计算和应用能力，为进一步学习奠定基础。具体内容与要求如下：
一、函数、极限与连续
(一)函数
1.理解函数的概念，会求函数的定义域、表达式及函数值，会建立应用问题的函数关系。
2.掌握函数的有界性、单调性、周期性和奇偶性。
3.理解分段函数、反函数和复合函数的概念。
4.掌握函数的四则运算与复合运算。
5.掌握基本初等函数的性质及其图形，理解初等函数的概念。
(二)极限
1.理解数列极限和函数极限(包括左极限和右极限)的概念。理解函数极限存在与左极限、右极限存在之间的关系。
2.理解数列极限和函数极限的性质。熟练掌握数列极限和函数极限的运算法则。
3.熟练掌握两个重要极限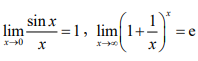专升本考试大纲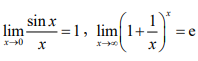，并会用它们求极限。
4.理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量与无穷大量的关系。会比较无穷小量的阶(高阶、低阶、同阶和等价)。会用等价无穷小量求极限。
(三)连续
1.理解函数连续性(包括左连续和右连续)的概念，掌握函数连续与左连续、右连续之间的关系。会求函数的间断点并判断其类型。
2.掌握连续函数的四则运算和复合运算。理解初等函数在其定义区间内的连续性。
3.会利用连续性求极限。
4.理解闭区间上连续函数的性质(有界性定理、最大值和最小值定理、介值定理、零点定理)，并会应用介值定理和零点定理解决简单问题。
二、一元函数微分学
(一)导数与微分
1.理解导数的概念及几何意义，会求平面曲线的切线方程和法线方程。理解函数的可导性与连续性之间的关系。
2.熟练掌握导数的四则运算法则和复合函数的求导法则，熟练掌握基本初等函数的导数公式。
3.掌握隐函数求导法、对数求导法。
4.了解高阶导数的概念，会求函数的二阶导数。
5.理解微分的概念，理解导数与微分的关系，掌握微分运算法则，会求函数的一阶微分。
(二)中值定理及导数的应用
1.理解罗尔定理、拉格朗日中值定理，掌握这两个定理的简单应用。
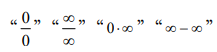
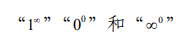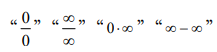
2.熟练掌握洛必达法则，会用洛必达法则求专升本考试大纲专升本考试大纲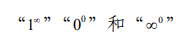型未定式的极限。
3.理解驻点、极值点和极值的概念，掌握用导数判断函数的单调性和求函数极值的方法，掌握函数最大值和最小值的求法及其应用。
4.了解曲线的凹凸性，会求曲线的拐点。
三、一元函数积分学
(一)不定积分
1.理解原函数与不定积分的概念，了解原函数存在定理，掌握不定积分的性质。
2.熟练掌握不定积分的基本公式。
3.熟练掌握不定积分的换元积分法和分部积分法。
4.掌握简单有理函数的不定积分的求法。
(二)定积分
1.理解定积分的概念及几何意义，了解可积的条件。
2.掌握定积分的性质及其应用。
3.理解积分上限的函数，会求它的导数，掌握牛顿-莱布尼茨公式。
4.熟练掌握定积分的换元积分法与分部积分法。
5.会用定积分表达和计算平面图形的面积。
Ⅱ.考试形式与题型范围
一、考试形式
考试采用闭卷、笔试形式。试卷满分100分，考试时间120分钟。
二、题型范围
选择题、填空题、判断题、计算题、解答题、证明题、应用题。

展开全文